算法简介

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。这是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

PS：此算法不能用于求负权图，要求所有边的权重都为非负值。

算法原理

dijkstra算法是基于贪心算法思想实现的。贪心算法即始终保持当前迭代解为当前最优解，即在当前一直的条件下包最最优解，若再次后的迭代中由于加入了新的条件使得产生了更优解来代替此前的最优解。通过不断迭代保证每次迭代结果都是当前的最后解，当迭代进行到最后一轮时，得到的解就是全局最优解。由于下一轮迭代会参考上一轮迭代的最优解，因此每一轮迭代的工作量基本一致，降低了整体工作的复杂性。

在最短路径的问题中，局部最优解即当前的最短路径或者说是在当前的已知条件下起点到其余各点的最短距离。关键就在于已知条件，这也是Dijkstra算法最精妙的地方。我们来解释一下。

对于Dijkstra算法，我们假设初始集合（也就是初始条件）不存在任何顶点的，即所有顶点之间是不存在任何路径的，即我们认为所有顶点之间的距离都是无穷大。那么开始加入新的条件，因为我们已知源点距源点距离最小，所以加入进去，并加入它的边，在该条件下，更新该源点到其余顶点的最短距离，选出没有加入到已知集合的距源点距离最小的点，此点最短距离也被确定了（因为其他路径都比这条路径大，无法通过其他路径间接到达这个顶点使得路径更小），然后加入该点与其余还未加入已知条件顶点的边，并以该点迭代刷新最短距离。再重复以上操作，直至所有顶点都加入已知条件集合。

算法步骤

1. 选择起点start和终点end；
2. 所有点除起点外加入未知集合，将起点加入已知集合，即至标志位为真，意为已确定该点到源点的最短路径；
3. 初始化计算，更新起点与其他各点的成本dis(start,n)；
4. 在未知集合中，选择dis(start,n)中值最小的点x，将x加入已知集合；
5. 在剩余顶点中，计算dis(start,n)>dis(start,x)+dis(x,n)。若真，则dis(start,n)=dis(start,x)+dis(x,n),此时start与n点路径经过x点。循环直至goal点加入已知列表，取得dis(start,goal)即为最短距离。

案例研究

以知乎回答为例，进行dijkstra最短路算法的案例分析，假设v1为源点，找从v1到其它节点的最短路径

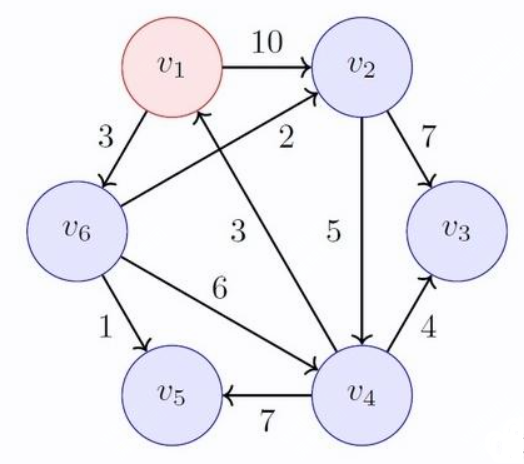
• 使用集合S存储已经找到的最短路径
• v1到自己显然最短，故为初始最短路径

第一轮：从v1出发，计算v1到其它节点的距离（无法连接则认为两点间的距离为正无穷）

• 全表寻找最小值，发现v1到v6最短为3
• S中添加一条最短路径：v1-v6
• v6列标红不再考虑

第二轮：从v1-v6出发，计算v1通过v6到达其它节点的距离

• 已知v1到v6的距离为3；v6可以到v2,v4,v5;因此，v1通过v6到其它节点的距离为3+n,n为6到各个节点的距离

• 在全表中找最小值（V6列已经删除），此时4为最小值，对应路径为v1—v6-v5
• 添加最短路径v1-v6-v5
• v5列不再考虑

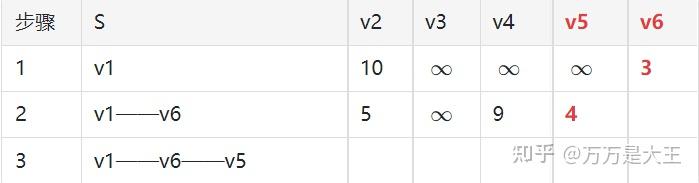
第三轮：从v1-v6-v5出发，计算v1通过v6及v5到达其它节点的距离

• 已知v1-v6-v5的长度为4；
• 发现，v5不能到现存的其他任何一个节点，因此距离全部为正无穷

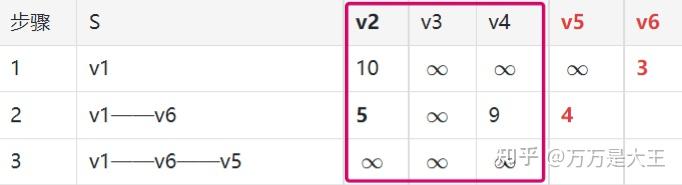
• 看全表（v5和v6已经删除）找最小值，5是最小值，对应的路径是v1-v6-v2
• 添加最短路径v1-v6-v2
• v2列不再考虑

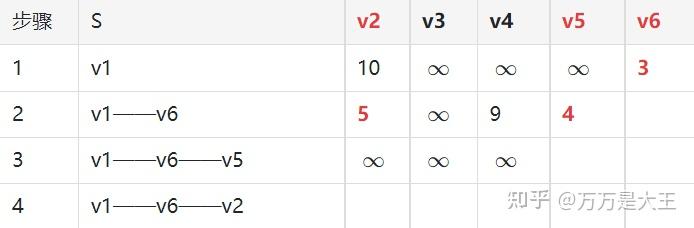
第四轮：从v1-v6-v2出发，计算v1通过v6及v2到其他节点的距离

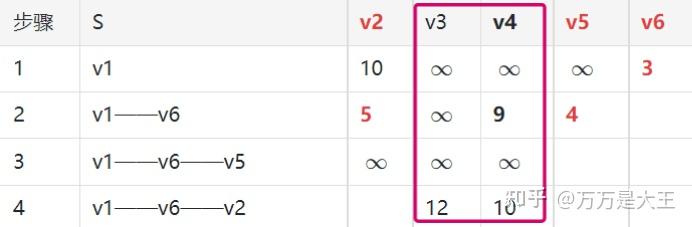
• 遍历全表（v2,v5和v6已经删除）发现，9最小，对应的路径为v1-v6-v4
• 添加最短路径v1-v6-v4
• v4列不再考虑

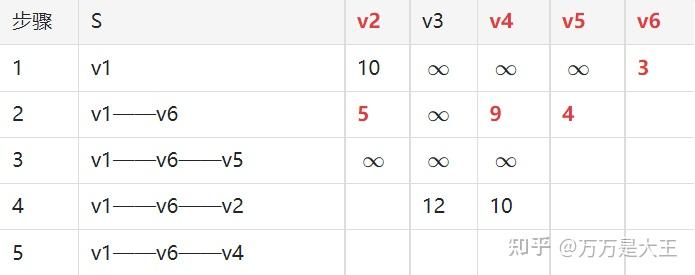
第五轮：从v1-v6-v4出发，计算v1通过v6及v4到其它节点的距离

• 遍历全表发现，12是现存的最小值，对应v1-v6-v2-v3路径最短
• 添加最短路径v1-v6-v2-v3
• v3列不再考虑

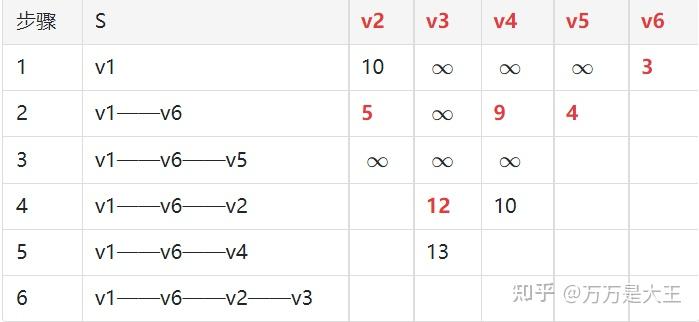
• 由于全部列已经删除，因此结束遍历
• 每列的标红值为v1到该节点的最短距离；从S列中找结尾为该列的路径
• eg：v2列标红值为5，说明v1到v2的最短距离为5
• S中结尾为v2，对应的路径为v1-v6-v2

代码实现

def dijkstra(graph, startIndex, path, cost, max):
    """
    求解各节点最短路径，获取path，和cost数组，
    path[i] 表示vi节点的前继节点索引，一直追溯到起点。
    cost[i] 表示vi节点的花费
    """
    lenth = len(graph)
    v = [0] * lenth
    # 初始化 path，cost，V
    for i in range(lenth):
        if i == startIndex:
            v[startIndex] = 1
        else:
            cost[i] = graph[startIndex][i]
            path[i] = (startIndex if (cost[i] < max) else -1)
    # print v, cost, path
    for i in range(1, lenth):
        minCost = max
        curNode = -1
        for w in range(lenth):
            if v[w] == 0 and cost[w] < minCost:
                minCost = cost[w]
                curNode = w
        # for 获取最小权值的节点
        if curNode == -1: break
        # 剩下都是不可通行的节点，跳出循环
        v[curNode] = 1
        for w in range(lenth):
            if v[w] == 0 and (graph[curNode][w] + cost[curNode] < cost[w]):
                cost[w] = graph[curNode][w] + cost[curNode] # 更新权值
                path[w] = curNode # 更新路径
        # for 更新其他节点的权值（距离）和路径
    return path

if __name__ == '__main__':
    max = 2147483647
    graph = [
        [max, 10, max, max, max, 3],
        [max, max, 7, 5, max, max],
        [max, max, max, max, max, max],
        [max, max, 4, max, 7, max],
        [max, max, max, max, max, max],
        [max, 2, max, 6, 1, max],
        ]
    path = [0] * 6
    cost = [0] * 6