定义
分支定界法是一种求解离散最优化问题的计算分析方法,由R.J达金和兰德-多伊在20世纪60年代初提出。这种方法通胀仅需计算和分析部分允许解,即可求得最优解。因此在求解分派问题和整数规划问题时常用此方法。该方法同样可以用于混合整数规划问题,以一般线性规划之单纯形法解得最优解后,将非整数之决策变量分割为最接近的两个整数,分裂条件加入原问题,形成两个子问题(或分支)分别求解,如此便可求得目标函数的上界或下界,从中寻得最优解。
基本思想
算法思想
分枝定界法是一个用途十分广泛的算法,运用这种算法的技巧性很强,不同类型的问题解法也各不相同。分支定界法的基本思想是对有约束条件的最优化问题的所有可行解(数目有限)空间进行搜索。该算法在具体执行时,把全部可行的解空间不断分割为越来越小的子集(称为分支),并为每个子集内的解的值计算一个下界或上界(称为定界)。在每次分支后,对凡是界限超出已知可行解值那些子集不再做进一步分支。这样,解的许多子集(即搜索树上的许多结点)就可以不予考虑了,从而缩小了搜索范围。这一过程一直进行到找出可行解为止,该可行解的值不大于任何子集的界限。因此这种算法一般可以求得最优解。
具体来说,求解一个约束条件较多的问题A,可以暂缓考虑部分条件,变换成问题B,先求B的最优解。B的最优解一定比A的好(或相当)。再将原来暂缓考虑的部分条件逐步插入问题B中,得到B的若干子问题,称为分枝。求解这些子问题,淘汰较差的解,直到所有暂缓考虑的部分条件全部插入为止。这时求得的最优解就是问题A的最优解。
分支节点的选择
对搜索树上的某些点必须作出分枝决策,即凡是界限小于迄今为止所有可行解最小下界的任何子集(节点),都有可能作为分枝的选择对象(对求最小值问题而言)。怎样选择搜索树上的节点作为下次分枝的节点呢?有两个原则:
-
从最小下界分枝(队列式FIFO分枝限界法):每次算完界限后,把搜索树上当前所有叶节点的界限进行比较。找出限界最小的节点,此结点即为下次分枝的结点。
- 优点:检查子问题较少,能较快地求得最佳解;
- 缺点:要存储很多叶节点的界限及对应的耗费矩阵,花费很多内存空间。
-
从最新产生的最小下界分枝(优先队列式分枝限界法):从最新产生的各子集中选择具有最小的下界的结点进行分枝。
- 优点:节省了空间;
- 缺点:需要较多的分枝运算,耗费的时间较多。
这两个原则更进一步说明了,在算法设计中的时空转换概念。分枝定界法已经成功地应用于求解整数规划问题、生产进度表问题、货郎担问题、选址问题、背包问题以及可行解的数目为有限的许多其它问题。对于不同的问题,分枝与界限的步骤和内容可能不同,但基本原理是一样的。
解法步骤
分支定界法的步骤如下所述:
-
如果问题的目标为最小化,则设定目前最优解的值Z=\infty;
-
根据分枝法则(Branching rule),从尚未被洞悉(Fathomed)节点(局部解)中选择一个节点,并在此节点的下一阶层中分为几个新的节点;
-
计算每一个新分枝出来节点的下限值(Lower bound,LB);
-
对每一节点进行洞悉条件测试,若节点满足以下任意一个条件,则此节点可洞悉而不再被考虑
- 此节点的下限值大于等于Z值;
- 已找到在此节点中,具最小下限值的可行解;若此条件成立,则需比较此可行解与Z值,若前者较小,则需更新Z值,以此为可行解的值;
- 此节点不可能包含可行解。
-
判断是否仍有尚未被洞悉的节点,如果有,则进行步骤二,如果已无尚未被洞悉的节点,则演算停止,并得到最优解

案例分析
求解下面的整数规划问题:
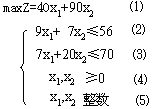
解:首先不考虑整数条件(5),求解相应的线性规划问题L,得到最优解:
$$x_1=4.81,x_2=1.82,Z_0=356$$
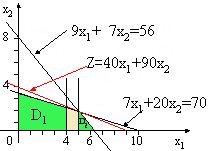
该解不是整数解。选择其中一个非整数变量,如x_1=4.81,对问题L分别增加约束条件:
x_1\leq4,x_1\geq5将问题L分解为两个子问题L_1,L_2(分枝),也就是去掉问题L不含整数解的一部分可行域,将原可行域D变为D_1,D_2两个部分,如图:
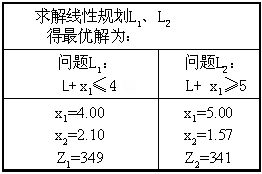
因为没有得到整数解,所以对L_1进行分解,增加约束x_1\leq2,x_1\geq3将L_1分解为问题L_3和L_4,并且求得最优解如下:

问题L_3的解已经是整数解,它的目标值Z_3=340,大于问题L_4的目标值,所以问题L_4已经无必要再分枝。但由于问题L_2的目标值Z_2大于Z_3,分解L_2还有可能产生更好的整数解,因此继续对L_2分枝。增加约束x_2\leq1,x_2\geq2将L_2分解成问题L_5和L_6,并求解,结果如下:

问题L_5的Z_5=308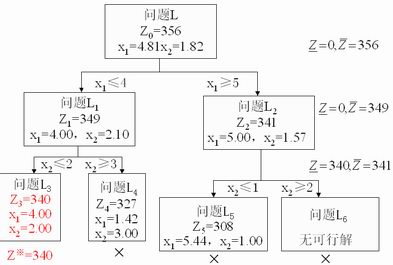



Comments NOTHING